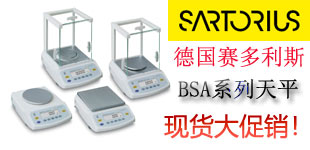
- 賽多利斯BSA系列電子天平,"放假" 大優惠!
青柠在线观看免费高清1,亚洲无码在线精品视频,日韩精品一区二区三区免费在线观看
|
|
| <tr id='jifwj'><strong id='jifwj'></strong><small id='jifwj'></small><button id='jifwj'></button><li id='jifwj'><noscript id='jifwj'><big id='jifwj'></big><dt id='jifwj'></dt></noscript></li></tr><ol id='jifwj'><option id='jifwj'><table id='jifwj'><blockquote id='jifwj'><tbody id='jifwj'></tbody></blockquote></table></option></ol><u id='jifwj'></u><kbd id='jifwj'><kbd id='jifwj'></kbd></kbd> |
|
|
|
|
|
<span id='jifwj'></span>
| |
|
| |
|
|
<ins id='jifwj'></ins> | |
|
| | <acronym id='jifwj'><em id='jifwj'></em><td id='jifwj'><div id='jifwj'></div></td></acronym><address id='jifwj'><big id='jifwj'><big id='jifwj'></big><legend id='jifwj'></legend></big></address>
|
<i id='jifwj'><div id='jifwj'><ins id='jifwj'></ins></div></i>|
<i id='jifwj'></i>
| |
|
<dl id='jifwj'></dl>|
|
|
|
|
| |
<dir id='jifwj'><del id='jifwj'><del id='jifwj'></del><pre id='jifwj'><pre id='jifwj'><option id='jifwj'><address id='jifwj'></address><bdo id='jifwj'><tr id='jifwj'><acronym id='jifwj'><pre id='jifwj'></pre></acronym><div id='jifwj'></div></tr></bdo></option></pre><small id='jifwj'><address id='jifwj'><u id='jifwj'><legend id='jifwj'><option id='jifwj'><abbr id='jifwj'></abbr><li id='jifwj'><pre id='jifwj'></pre></li></option></legend><select id='jifwj'></select></u></address></small></pre></del><sup id='jifwj'></sup><blockquote id='jifwj'><dt id='jifwj'></dt></blockquote><blockquote id='jifwj'></blockquote></dir><tt id='jifwj'></tt><u id='jifwj'><tt id='jifwj'><form id='jifwj'></form></tt><td id='jifwj'><dt id='jifwj'></dt></td></u>
|
| |
| |
<code id='jifwj'><i id='jifwj'><q id='jifwj'><legend id='jifwj'><pre id='jifwj'><style id='jifwj'><acronym id='jifwj'><i id='jifwj'><form id='jifwj'><option id='jifwj'><center id='jifwj'></center></option></form></i></acronym></style><tt id='jifwj'></tt></pre></legend></q></i></code><center id='jifwj'></center> | | |
| |
|
|
| |
|
|
|
| | |
|
<style id='jifwj'></style><sub id='jifwj'><dfn id='jifwj'><abbr id='jifwj'><big id='jifwj'><bdo id='jifwj'></bdo></big></abbr></dfn></sub> | <dir id='jifwj'></dir> |
- 英國艾德姆經濟型系列電子天平,優惠大特價!
青柠在线观看免费高清1,亚洲无码在线精品视频,日韩精品一区二区三区免费在线观看
|
|
| <tr id='jifwj'><strong id='jifwj'></strong><small id='jifwj'></small><button id='jifwj'></button><li id='jifwj'><noscript id='jifwj'><big id='jifwj'></big><dt id='jifwj'></dt></noscript></li></tr><ol id='jifwj'><option id='jifwj'><table id='jifwj'><blockquote id='jifwj'><tbody id='jifwj'></tbody></blockquote></table></option></ol><u id='jifwj'></u><kbd id='jifwj'><kbd id='jifwj'></kbd></kbd> |
<code id='jifwj'><strong id='jifwj'></strong></code> |
|
|
|
<span id='jifwj'></span>
| |
|
| | |
|
|
<ins id='jifwj'></ins> | |
|
|
| | <acronym id='jifwj'><em id='jifwj'></em><td id='jifwj'><div id='jifwj'></div></td></acronym><address id='jifwj'><big id='jifwj'><big id='jifwj'></big><legend id='jifwj'></legend></big></address>
|
<i id='jifwj'><div id='jifwj'><ins id='jifwj'></ins></div></i>|
|
|
<i id='jifwj'></i>
| |
|
<dl id='jifwj'></dl>|
|
|
|
|
| |
<dir id='jifwj'><del id='jifwj'><del id='jifwj'></del><pre id='jifwj'><pre id='jifwj'><option id='jifwj'><address id='jifwj'></address><bdo id='jifwj'><tr id='jifwj'><acronym id='jifwj'><pre id='jifwj'></pre></acronym><div id='jifwj'></div></tr></bdo></option></pre><small id='jifwj'><address id='jifwj'><u id='jifwj'><legend id='jifwj'><option id='jifwj'><abbr id='jifwj'></abbr><li id='jifwj'><pre id='jifwj'></pre></li></option></legend><select id='jifwj'></select></u></address></small></pre></del><sup id='jifwj'></sup><blockquote id='jifwj'><dt id='jifwj'></dt></blockquote><blockquote id='jifwj'></blockquote></dir><tt id='jifwj'></tt><u id='jifwj'><tt id='jifwj'><form id='jifwj'></form></tt><td id='jifwj'><dt id='jifwj'></dt></td></u>
|
| |
| |
<code id='jifwj'><i id='jifwj'><q id='jifwj'><legend id='jifwj'><pre id='jifwj'><style id='jifwj'><acronym id='jifwj'><i id='jifwj'><form id='jifwj'><option id='jifwj'><center id='jifwj'></center></option></form></i></acronym></style><tt id='jifwj'></tt></pre></legend></q></i></code><center id='jifwj'></center> | | |
| |
|
|
| |
|
|
|
| | |
|
<style id='jifwj'></style><sub id='jifwj'><dfn id='jifwj'><abbr id='jifwj'><big id='jifwj'><bdo id='jifwj'></bdo></big></abbr></dfn></sub> | <dir id='jifwj'></dir> |
- 艾德姆十萬分之一天平“性價比之王”大促銷!
青柠在线观看免费高清1,亚洲无码在线精品视频,日韩精品一区二区三区免费在线观看
|
|
| <tr id='jifwj'><strong id='jifwj'></strong><small id='jifwj'></small><button id='jifwj'></button><li id='jifwj'><noscript id='jifwj'><big id='jifwj'></big><dt id='jifwj'></dt></noscript></li></tr><ol id='jifwj'><option id='jifwj'><table id='jifwj'><blockquote id='jifwj'><tbody id='jifwj'></tbody></blockquote></table></option></ol><u id='jifwj'></u><kbd id='jifwj'><kbd id='jifwj'></kbd></kbd> |
<code id='jifwj'><strong id='jifwj'></strong></code> |
|
|
|
<span id='jifwj'></span>
| |
|
| | |
|
|
<ins id='jifwj'></ins> | |
|
|
| | <acronym id='jifwj'><em id='jifwj'></em><td id='jifwj'><div id='jifwj'></div></td></acronym><address id='jifwj'><big id='jifwj'><big id='jifwj'></big><legend id='jifwj'></legend></big></address>
|
<i id='jifwj'><div id='jifwj'><ins id='jifwj'></ins></div></i>|
|
|
<i id='jifwj'></i>
| |
|
<dl id='jifwj'></dl>|
|
|
|
|
| |
<dir id='jifwj'><del id='jifwj'><del id='jifwj'></del><pre id='jifwj'><pre id='jifwj'><option id='jifwj'><address id='jifwj'></address><bdo id='jifwj'><tr id='jifwj'><acronym id='jifwj'><pre id='jifwj'></pre></acronym><div id='jifwj'></div></tr></bdo></option></pre><small id='jifwj'><address id='jifwj'><u id='jifwj'><legend id='jifwj'><option id='jifwj'><abbr id='jifwj'></abbr><li id='jifwj'><pre id='jifwj'></pre></li></option></legend><select id='jifwj'></select></u></address></small></pre></del><sup id='jifwj'></sup><blockquote id='jifwj'><dt id='jifwj'></dt></blockquote><blockquote id='jifwj'></blockquote></dir><tt id='jifwj'></tt><u id='jifwj'><tt id='jifwj'><form id='jifwj'></form></tt><td id='jifwj'><dt id='jifwj'></dt></td></u>
|
| |
| |
<code id='jifwj'><i id='jifwj'><q id='jifwj'><legend id='jifwj'><pre id='jifwj'><style id='jifwj'><acronym id='jifwj'><i id='jifwj'><form id='jifwj'><option id='jifwj'><center id='jifwj'></center></option></form></i></acronym></style><tt id='jifwj'></tt></pre></legend></q></i></code><center id='jifwj'></center> | | |
| |
|
|
| |
|
|
|
| | |
|
<style id='jifwj'></style><sub id='jifwj'><dfn id='jifwj'><abbr id='jifwj'><big id='jifwj'><bdo id='jifwj'></bdo></big></abbr></dfn></sub> | <dir id='jifwj'></dir>